Definition
In geometry, supplementary describes two angles whose measures add up to exactly 180 degrees. These angles are called supplementary angles, and together they form a straight line.
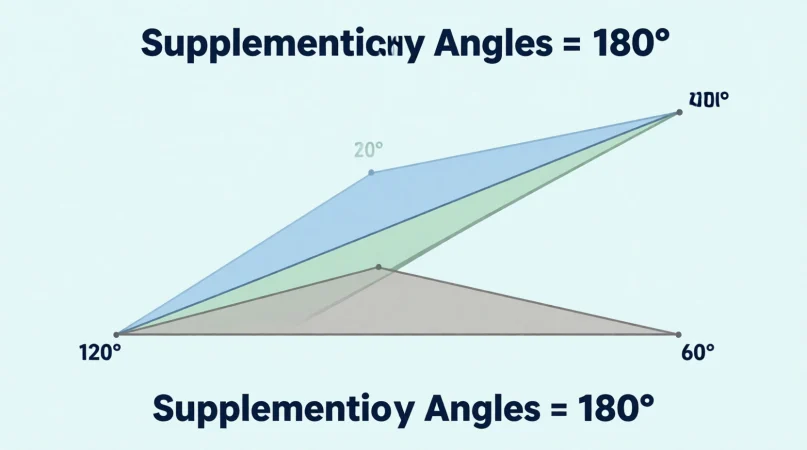
If Angle A is 120° and Angle B is 60°, they are supplementary because 120° + 60° = 180°.
Geometry terms can sound intimidating at first—but supplementary is actually one of the most practical and visual ideas in math. Once you understand it, you’ll start spotting supplementary angles everywhere: on straight roads, open books, clock faces, and even in everyday designs 📐.
This guide breaks the concept down in a friendly, student-safe, and teacher-approved way—perfect for learners, parents, and educators alike.
What Does Supplementary Mean in Geometry?
In geometry, supplementary refers to a relationship between two angles, not a single angle on its own.
Supplementary Angles Explained Simply
Two angles are supplementary when:
- Their total measure equals 180°
- They often (but not always) sit next to each other
- Together, they form a straight line
Quick Formula
Angle 1 + Angle 2 = 180°
That’s it. No tricks, no hidden steps.
Origin and Meaning of the Word “Supplementary”
Understanding the word itself makes the concept easier to remember.
Word Origin
- Comes from the Latin word supplementum
- Meaning: to fill up or to complete
In geometry, one angle supplements another by filling in what’s needed to reach 180°.
Why This Matters
When students understand the language logic, geometry becomes less about memorizing rules and more about recognizing patterns.
Why Supplementary Angles Matter in Geometry
Supplementary angles are a core concept in geometry because they help explain how lines, shapes, and angles interact.
Where They’re Used
- Solving angle problems
- Understanding straight lines
- Working with parallel lines
- Preparing for algebra and trigonometry
- Standardized math tests and exams
You’ll see supplementary angles repeatedly as geometry becomes more advanced.
Types of Supplementary Angles
Not all supplementary angles look the same. Let’s break them into simple categories.
1. Adjacent Supplementary Angles
- Angles share a common side
- They sit next to each other
- Together they form a straight line
Example:
- One angle = 110°
- The other = 70°
- They touch and add to 180°
2. Non-Adjacent Supplementary Angles
- Angles are separate
- They don’t touch
- They still add up to 180°
Example:
- Angle A = 40°
- Angle B = 140°
- Located in different parts of the diagram
Both types are equally valid in geometry problems.
Supplementary vs Complementary Angles
This is one of the most common sources of confusion, so let’s clear it up cleanly.
Key Differences at a Glance
| Term | Total Degrees | Meaning |
|---|---|---|
| Supplementary angles | 180° | Form a straight line |
| Complementary angles | 90° | Form a right angle |
Memory Tip
- Supplementary = Straight line = 180°
- Complementary = Corner (right angle) = 90°
Real-World Examples of Supplementary Angles
Supplementary angles aren’t just classroom ideas—they show up in real life all the time.
Everyday Examples
- 🛣️ A straight road intersection
- 📖 An open book laid flat
- 🕒 The 6 o’clock position on a clock
- 📐 Hinges on doors
- 🧱 Bricks laid in straight rows
Once you start looking, you’ll notice them everywhere.
Geometry Examples With Context
Let’s see how supplementary is used in real math situations.
Friendly Classroom Example 😊
A teacher says:
“If one angle is 125°, what is its supplementary angle?”
Solution:
180° − 125° = 55°
Neutral Math Problem
Two angles form a straight line. One angle measures 68°. Find the other.
Answer:
180° − 68° = 112°
Test or Exam Context ⚠️
If angles are supplementary and one angle is x + 30°, the other is 2x − 10°, find x.
Solution Steps:
- (x + 30) + (2x − 10) = 180
- 3x + 20 = 180
- x = 53.33
Labeled Example Table: Supplementary Angles
| Angle A | Angle B | Supplementary? | Why |
|---|---|---|---|
| 90° | 90° | Yes | 90 + 90 = 180 |
| 45° | 135° | Yes | Add to 180 |
| 60° | 120° | Yes | Straight line |
| 80° | 80° | No | Total is 160 |
| 30° | 150° | Yes | Complete straight angle |
Common Geometry Situations Involving Supplementary Angles
Supplementary angles often appear alongside other geometry rules.
Linear Pairs
- Two adjacent angles
- Share a side
- Form a straight line
- Always supplementary
Parallel Lines and Transversals
When a line crosses parallel lines:
- Same-side interior angles are supplementary
- Used heavily in proofs and exams
Alternate Meanings of “Supplementary”
Outside geometry, supplementary has broader meanings.
General English Meaning
- Something added to complete or enhance
- Extra or additional material
Examples:
- Supplementary reading
- Supplementary income
- Supplementary instructions
In geometry, the meaning stays strict and numerical—always related to 180°.
Polite and Professional Alternatives in Writing
In academic or teaching contexts, you might see alternatives like:
- Angles that sum to 180°
- Linear angle pairs
- Straight-angle pairs
These are often used to clarify explanations for beginners.
Usage Tips for Students and Teachers
For Students
- Always check the total
- Don’t assume angles must touch
- Look for straight lines in diagrams
For Teachers
- Use visual examples
- Connect to real-life objects
- Reinforce with complementary comparisons
FAQs
1. What does supplementary mean in geometry?
It means two angles add up to exactly 180 degrees.
2. Do supplementary angles have to touch?
No. They can be adjacent or separate.
3. Can two right angles be supplementary?
Yes. 90° + 90° = 180°.
4. Are supplementary angles always a straight line?
They often form a straight line, but not always visually.
5. What is a linear pair?
Two adjacent supplementary angles that form a straight line.
6. How do you find a missing supplementary angle?
Subtract the known angle from 180°.
7. Are supplementary and complementary the same?
No. Complementary angles add to 90°, supplementary add to 180°.
8. Why are supplementary angles important?
They help solve geometry problems, proofs, and real-world measurements.
Conclusion
Understanding what supplementary means in geometry is a big step toward mastering angles and straight-line relationships. Simply put, supplementary angles are two angles that add up to 180 degrees, often forming a straight line. Once you lock this idea in, many geometry problems become easier and faster to solve.
Remember these keys:
- Supplementary angles always total 180°
- They can be adjacent or non-adjacent
- A linear pair is a common example of supplementary angles
- They are different from complementary angles, which add up to 90°
Whether you’re a student preparing for exams, a teacher explaining angle rules, or a parent helping with homework, knowing how supplementary angles work builds confidence and clarity in geometry. Keep an eye out for straight lines in diagrams and you’ll spot supplementary angles instantly 📐✨

Megan Lewis is a passionate and experienced content writer specializing in creating engaging and well-researched content. She excels at producing clear, informative, and reader-focused content that not only ranks well on search engines but also delivers real value to audiences.